Iterators and Generators¶
In the section on loops we introduced the range function, and said that you should think about it as creating a list of numbers. In Python 2.X this is exactly what it does. In Python 3.X this is not what it does. Instead it creates the numbers one at a time. The difference in speed and memory usage is enormous for very large lists - examples are given here and
here.
We can recreate one of the examples from Meuer’s slides in detail:
[1]:
def naivesum_list(N):
"""
Naively sum the first N integers
"""
A = 0
for i in list(range(N + 1)):
A += i
return A
We will now see how much memory this uses:
[2]:
%load_ext memory_profiler
[3]:
%memit naivesum_list(10**4)
peak memory: 32.38 MiB, increment: 0.50 MiB
[4]:
%memit naivesum_list(10**5)
peak memory: 35.95 MiB, increment: 3.57 MiB
[5]:
%memit naivesum_list(10**6)
peak memory: 70.75 MiB, increment: 34.79 MiB
[6]:
%memit naivesum_list(10**7)
peak memory: 426.25 MiB, increment: 382.75 MiB
[7]:
%memit naivesum_list(10**8)
peak memory: 3856.96 MiB, increment: 3744.59 MiB
We see that the memory usage is growing very rapidly - as the list gets large it’s growing as 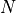 .
.
Instead we can use the range function that yields one integer at a time:
[8]:
def naivesum(N):
"""
Naively sum the first N integers
"""
A = 0
for i in range(N + 1):
A += i
return A
[9]:
%memit naivesum(10**4)
peak memory: 34.35 MiB, increment: 0.13 MiB
[10]:
%memit naivesum(10**5)
peak memory: 34.38 MiB, increment: 0.01 MiB
[11]:
%memit naivesum(10**6)
peak memory: 34.40 MiB, increment: 0.01 MiB
[12]:
%memit naivesum(10**7)
peak memory: 34.41 MiB, increment: 0.00 MiB
[13]:
%memit naivesum(10**8)
peak memory: 34.41 MiB, increment: 0.00 MiB
We see that the memory usage is unchanged with 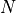 , making it practical to run much larger calculations.
, making it practical to run much larger calculations.
Iterators¶
The range function is returning an iterator here. This is an object - a general thing - that represents a stream, or a sequence, of data. The iterator knows how to create the first element of the stream, and it knows how to get the next element. It does not, in general, need to know all of the elements at once.
As we’ve seen above this can save a lot of memory. It can also save time: the code does not need to construct all of the members of the sequence before starting, and it’s quite possible you don’t need all of them (think about the “Shortest published mathematical paper” exercise).
An iterator such as range is very useful, and there’s a lot more useful ways to work with iterators in the itertools module. These functions that return iterators, such as range, are called generators, and it’s useful to be able to make your own.
Making your own generators¶
Let’s look at an example: finding all primes less than 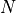 that can be written in the form
that can be written in the form 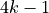 , where
, where 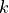 is an integer.
is an integer.
We’re going to need to calculate all prime numbers less than or equal to 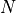 . We could write a function that returns all these numbers as a list. However, if
. We could write a function that returns all these numbers as a list. However, if 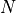 gets large then this will be expensive, both in time and memory. As we only need one number at a time, we can use a generator.
gets large then this will be expensive, both in time and memory. As we only need one number at a time, we can use a generator.
[14]:
def all_primes(N):
"""
Return all primes less than or equal to N.
Parameters
----------
N : int
Maximum number
Returns
-------
prime : generator
Prime numbers
"""
primes = []
for n in range(2, N+1):
is_n_prime = True
for p in primes:
if n%p == 0:
is_n_prime = False
break
if is_n_prime:
primes.append(n)
yield n
This code needs careful examination. First it defines the list of all prime numbers that it currently knows, primes (which is initially empty). Then it loops through all integers 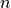 from
from 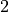 to
to 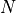 (ignoring
(ignoring 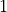 as we know it’s not prime).
as we know it’s not prime).
Inside this loop it initially assumes that 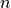 is prime. It then checks if any of the known primes exactly divides
is prime. It then checks if any of the known primes exactly divides 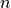 (
(n%p == 0 checks if 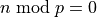 ). As soon as it finds such a prime divisor it knows that
). As soon as it finds such a prime divisor it knows that 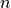 is not prime it resets the assumption with this new knowledge, then
is not prime it resets the assumption with this new knowledge, then breaks out of the loop. This statement stops the for p in primes loop early, as we don’t need to look at later primes.
If no known prime ever divides 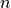 then at the end of the
then at the end of the for p in primes loop we will still have is_n_prime being True. In this case we must have 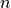 being prime, so we add it to the list of known primes and return it.
being prime, so we add it to the list of known primes and return it.
It is precisely this point which makes the code above define a generator. We return the value of the prime number found
- using the
yieldkeyword, not thereturnkeyword, and - we return the value as soon as it is known.
It is the use of the yield keyword that makes this function a generator.
This means that only the latest prime number is stored for return.
To use the iterator within a loop, we code it in the same way as with the range function:
[15]:
print("All prime numbers less than or equal to 20:")
for p in all_primes(20):
print(p)
All prime numbers less than or equal to 20:
2
3
5
7
11
13
17
19
To see what the generator is actually doing, we can step through it one call at a time using the built in next function:
[16]:
a = all_primes(10)
[17]:
next(a)
[17]:
2
[18]:
next(a)
[18]:
3
[19]:
next(a)
[19]:
5
[20]:
next(a)
[20]:
7
[21]:
next(a)
---------------------------------------------------------------------------
StopIteration Traceback (most recent call last)
<ipython-input-21-3f6e2eea332d> in <module>()
----> 1 next(a)
StopIteration:
So, when the generator gets to the end of its iteration it raises an exception. As seen in previous sections, we could surround the next call with a try block to capture the StopIteration so that we can continue after it finishes. This is effectively what the for loop is doing.
We can now find all primes (less than or equal to 100, for example) that have the form 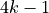 using
using
[22]:
for p in all_primes(100):
if (1+p)%4 == 0:
print("The prime {} is 4 * {} - 1.".format(p, int((1+p)/4)))
The prime 3 is 4 * 1 - 1.
The prime 7 is 4 * 2 - 1.
The prime 11 is 4 * 3 - 1.
The prime 19 is 4 * 5 - 1.
The prime 23 is 4 * 6 - 1.
The prime 31 is 4 * 8 - 1.
The prime 43 is 4 * 11 - 1.
The prime 47 is 4 * 12 - 1.
The prime 59 is 4 * 15 - 1.
The prime 67 is 4 * 17 - 1.
The prime 71 is 4 * 18 - 1.
The prime 79 is 4 * 20 - 1.
The prime 83 is 4 * 21 - 1.
Exercise : twin primes¶
A twin prime is a pair 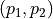 such that both
such that both 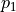 and
and 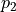 are prime and
are prime and 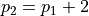 .
.
Exercise 1¶
Write a generator that returns twin primes. You can use the generators above, and may want to look at the itertools module together with its recipes, particularly the pairwise recipe.
Exercise 2¶
Find how many twin primes there are with 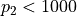 .
.
Exercise 3¶
Let 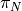 be the number of twin primes such that
be the number of twin primes such that 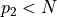 . Plot how
. Plot how 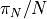 varies with
varies with 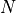 for
for 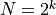 and
and 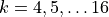 . (You should use a logarithmic scale where appropriate!)
. (You should use a logarithmic scale where appropriate!)
Exercise : a basis for the polynomials¶
In the section on classes we defined a Monomial class to represent a polynomial with leading coefficient 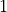 . As the
. As the 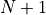 monomials
monomials 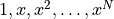 form a basis for the vector space of polynomials of order
form a basis for the vector space of polynomials of order 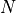 ,
, 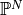 , we can use the
, we can use the Monomial class to return this basis.
Exercise 1¶
Define a generator that will iterate through this basis of 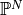 and test it on
and test it on 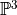 .
.
Exercise 2¶
An alternative basis is given by the monomials
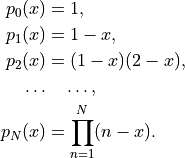
Define a generator that will iterate through this basis of 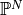 and test it on
and test it on 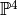 .
.
Exercise 3¶
Use these generators to write another generator that produces a basis of 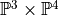 .
.