Exceptions and Testing¶

Things go wrong when programming all the time. Some of these “problems” are errors that stop the program from making sense. Others are problems that stop the program from working in specific, special cases. These “problems” may be real, or we may want to treat them as special cases that don’t stop the program from running.

These special cases can be dealt with using exceptions.

Exceptions¶

Let’s define a function that divides two numbers.

[1]:

from __future__ import division

[2]:

def divide(numerator, denominator):
    """
    Divide two numbers.

    Parameters
    ----------

    numerator: float
        numerator
    denominator: float
        denominator

    Returns
    -------

    fraction: float
        numerator / denominator
    """
    return numerator / denominator

[3]:

print(divide(4.0, 5.0))

0.8

But what happens if we try something really stupid?

[4]:

print(divide(4.0, 0.0))

---------------------------------------------------------------------------
ZeroDivisionError                         Traceback (most recent call last)
<ipython-input-4-316ba9717160> in <module>()
----> 1 print(divide(4.0, 0.0))

<ipython-input-2-f5b027ed84cf> in divide(numerator, denominator)
     17         numerator / denominator
     18     """
---> 19     return numerator / denominator

ZeroDivisionError: float division by zero

So, the code works fine until we pass in input that we shouldn’t. When we do, this causes the code to stop. To show how this can be a problem, consider the loop:

[5]:

denominators = [1.0, 0.0, 3.0, 5.0]
for denominator in denominators:
    print(divide(4.0, denominator))

4.0

---------------------------------------------------------------------------
ZeroDivisionError                         Traceback (most recent call last)
<ipython-input-5-05c6ef547bde> in <module>()
      1 denominators = [1.0, 0.0, 3.0, 5.0]
      2 for denominator in denominators:
----> 3     print(divide(4.0, denominator))

<ipython-input-2-f5b027ed84cf> in divide(numerator, denominator)
     17         numerator / denominator
     18     """
---> 19     return numerator / denominator

ZeroDivisionError: float division by zero

There are three sensible results, but we only get the first.

There are many more complex, real cases where it’s not obvious that we’re doing something wrong ahead of time. In this case, we want to be able to try running the code and catch errors without stopping the code. This can be done in Python:

[6]:

try:
    print(divide(4.0, 0.0))
except ZeroDivisionError:
    print("Dividing by zero is a silly thing to do!")

Dividing by zero is a silly thing to do!

[7]:

denominators = [1.0, 0.0, 3.0, 5.0]
for denominator in denominators:
    try:
        print(divide(4.0, denominator))
    except ZeroDivisionError:
        print("Dividing by zero is a silly thing to do!")

4.0
Dividing by zero is a silly thing to do!
1.3333333333333333
0.8

The idea here is given by the names. Python will try to execute the code inside the try block. This is just like an if or a for block: each command that is indented in that block will be executed in order.

If, and only if, an error arises then the except block will be checked. If the error that is produced matches the one listed then instead of stopping, the code inside the except block will be run instead.

To show how this works with different errors, consider a different silly error:

[8]:

try:
    print(divide(4.0, "zero"))
except ZeroDivisionError:
    print("Dividing by zero is a silly thing to do!")

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-8-220d79bf294a> in <module>()
      1 try:
----> 2     print(divide(4.0, "zero"))
      3 except ZeroDivisionError:
      4     print("Dividing by zero is a silly thing to do!")

<ipython-input-2-f5b027ed84cf> in divide(numerator, denominator)
     17         numerator / denominator
     18     """
---> 19     return numerator / denominator

TypeError: unsupported operand type(s) for /: 'float' and 'str'

We see that, as it makes no sense to divide by a string, we get a TypeError instead of a ZeroDivisionError. We could catch both errors:

[9]:

try:
    print(divide(4.0, "zero"))
except ZeroDivisionError:
    print("Dividing by zero is a silly thing to do!")
except TypeError:
    print("Dividing by a string is a silly thing to do!")

Dividing by a string is a silly thing to do!

We could catch any error:

[10]:

try:
    print(divide(4.0, "zero"))
except:
    print("Some error occured")

Some error occured

This doesn’t give us much information, and may lose information that we need in order to handle the error. We can capture the exception to a variable, and then use that variable:

[11]:

try:
    print(divide(4.0, "zero"))
except (ZeroDivisionError, TypeError) as exception:
    print("Some error occured: {}".format(exception))

Some error occured: unsupported operand type(s) for /: 'float' and 'str'

Here we have caught two possible types of error within the tuple (which must, in this case, have parantheses) and captured the specific error in the variable exception. This variable can then be used: here we just print it out.

Normally best practise is to be as specific as possible on the error you are trying to catch.

Extending the logic¶

Sometimes you may want to perform an action only if an error did not occur. For example, let’s suppose we wanted to store the result of dividing 4 by a divisor, and also store the divisor, but only if the divisor is valid.

One way of doing this would be the following:

[12]:

denominators = [1.0, 0.0, 3.0, "zero", 5.0]
results = []
divisors = []
for denominator in denominators:
    try:
        result = divide(4.0, denominator)
    except (ZeroDivisionError, TypeError) as exception:
        print("Error of type {} for denominator {}".format(exception, denominator))
    else:
        results.append(result)
        divisors.append(denominator)
print(results)
print(divisors)

Error of type float division by zero for denominator 0.0
Error of type unsupported operand type(s) for /: 'float' and 'str' for denominator zero
[4.0, 1.3333333333333333, 0.8]
[1.0, 3.0, 5.0]

The statements in the else block are only run if the try block succeeds. If it doesn’t - if the statements in the try block raise an exception - then the statements in the else block are not run.

Exceptions in your own code¶

Sometimes you don’t want to wait for the code to break at a low level, but instead stop when you know things are going to go wrong. This is usually because you can be more informative about what’s going wrong. Here’s a slightly artificial example:

[13]:

def divide_sum(numerator, denominator1, denominator2):
    """
    Divide a number by a sum.

    Parameters
    ----------

    numerator: float
        numerator
    denominator1: float
        Part of the denominator
    denominator2: float
        Part of the denominator

    Returns
    -------

    fraction: float
        numerator / (denominator1 + denominator2)
    """

    return numerator / (denominator1 + denominator2)

[14]:

divide_sum(1, 1, -1)

---------------------------------------------------------------------------
ZeroDivisionError                         Traceback (most recent call last)
<ipython-input-14-a77bb3466659> in <module>()
----> 1 divide_sum(1, 1, -1)

<ipython-input-13-0b7e8c50456d> in divide_sum(numerator, denominator1, denominator2)
     20     """
     21
---> 22     return numerator / (denominator1 + denominator2)

ZeroDivisionError: division by zero

It should be obvious to the code that this is going to go wrong. Rather than letting the code hit the ZeroDivisionError exception automatically, we can raise it ourselves, with a more meaningful error message:

[15]:

def divide_sum(numerator, denominator1, denominator2):
    """
    Divide a number by a sum.

    Parameters
    ----------

    numerator: float
        numerator
    denominator1: float
        Part of the denominator
    denominator2: float
        Part of the denominator

    Returns
    -------

    fraction: float
        numerator / (denominator1 + denominator2)
    """

    if (denominator1 + denominator2) == 0:
        raise ZeroDivisionError("The sum of denominator1 and denominator2 is zero!")

    return numerator / (denominator1 + denominator2)

[16]:

divide_sum(1, 1, -1)

---------------------------------------------------------------------------
ZeroDivisionError                         Traceback (most recent call last)
<ipython-input-16-a77bb3466659> in <module>()
----> 1 divide_sum(1, 1, -1)

<ipython-input-15-49244a562615> in divide_sum(numerator, denominator1, denominator2)
     21
     22     if (denominator1 + denominator2) == 0:
---> 23         raise ZeroDivisionError("The sum of denominator1 and denominator2 is zero!")
     24
     25     return numerator / (denominator1 + denominator2)

ZeroDivisionError: The sum of denominator1 and denominator2 is zero!

There are a large number of standard exceptions in Python, and most of the time you should use one of those, combined with a meaningful error message. One is particularly useful: NotImplementedError.

This exception is used when the behaviour the code is about to attempt makes no sense, is not defined, or similar. For example, consider computing the roots of the quadratic equation, but restricting to only real solutions. Using the standard formula

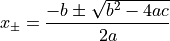
$x_{\pm} = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

we know that this only makes sense if 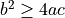$b^2 \ge 4ac$ . We put this in code as:

[17]:

from math import sqrt

def real_quadratic_roots(a, b, c):
    """
    Find the real roots of the quadratic equation a x^2 + b x + c = 0, if they exist.

    Parameters
    ----------

    a : float
        Coefficient of x^2
    b : float
        Coefficient of x^1
    c : float
        Coefficient of x^0

    Returns
    -------

    roots : tuple
        The roots

    Raises
    ------

    NotImplementedError
        If the roots are not real.
    """

    discriminant = b**2 - 4.0*a*c
    if discriminant < 0.0:
        raise NotImplementedError("The discriminant is {} < 0. "
                                  "No real roots exist.".format(discriminant))

    x_plus = (-b + sqrt(discriminant)) / (2.0*a)
    x_minus = (-b - sqrt(discriminant)) / (2.0*a)

    return x_plus, x_minus

[18]:

print(real_quadratic_roots(1.0, 5.0, 6.0))

(-2.0, -3.0)

[19]:

real_quadratic_roots(1.0, 1.0, 5.0)

---------------------------------------------------------------------------
NotImplementedError                       Traceback (most recent call last)
<ipython-input-19-0fda03c09b58> in <module>()
----> 1 real_quadratic_roots(1.0, 1.0, 5.0)

<ipython-input-17-f4ffff0c1b94> in real_quadratic_roots(a, b, c)
     31     if discriminant < 0.0:
     32         raise NotImplementedError("The discriminant is {} < 0. "
---> 33                                   "No real roots exist.".format(discriminant))
     34
     35     x_plus = (-b + sqrt(discriminant)) / (2.0*a)

NotImplementedError: The discriminant is -19.0 < 0. No real roots exist.

Testing¶

How do we know if our code is working correctly? It is not when the code runs and returns some value: as seen above, there may be times where it makes sense to stop the code even when it is correct, as it is being used incorrectly. We need to test the code to check that it works.

Unit testing is the idea of writing many small tests that check if simple cases are behaving correctly. Rather than trying to prove that the code is correct in all cases (which could be very hard), we check that it is correct in a number of tightly controlled cases (which should be more straightforward). If we later find a problem with the code, we add a test to cover that case.

Consider a function solving for the real roots of the quadratic equation again. This time, if there are no real roots we shall return None (to say there are no roots) instead of raising an exception.

[20]:

from math import sqrt

def real_quadratic_roots(a, b, c):
    """
    Find the real roots of the quadratic equation a x^2 + b x + c = 0, if they exist.

    Parameters
    ----------

    a : float
        Coefficient of x^2
    b : float
        Coefficient of x^1
    c : float
        Coefficient of x^0

    Returns
    -------

    roots : tuple or None
        The roots
    """

    discriminant = b**2 - 4.0*a*c
    if discriminant < 0.0:
        return None

    x_plus = (-b + sqrt(discriminant)) / (2.0*a)
    x_minus = (-b + sqrt(discriminant)) / (2.0*a)

    return x_plus, x_minus

First we check what happens if there are imaginary roots, using 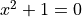$x^2 + 1 = 0$ :

[21]:

print(real_quadratic_roots(1, 0, 1))

None

As we wanted, it has returned None. We also check what happens if the roots are zero, using 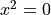$x^2 = 0$ :

[22]:

print(real_quadratic_roots(1, 0, 0))

(0.0, 0.0)

We get the expected behaviour. We also check what happens if the roots are real, using 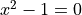$x^2 - 1 = 0$ which has roots $\pm 1$ :

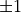[23]:

print(real_quadratic_roots(1, 0, -1))

(1.0, 1.0)

Something has gone wrong. Looking at the code, we see that the x_minus line has been copied and pasted from the x_plus line, without changing the sign correctly. So we fix that error:

[24]:

from math import sqrt

def real_quadratic_roots(a, b, c):
    """
    Find the real roots of the quadratic equation a x^2 + b x + c = 0, if they exist.

    Parameters
    ----------

    a : float
        Coefficient of x^2
    b : float
        Coefficient of x^1
    c : float
        Coefficient of x^0

    Returns
    -------

    roots : tuple or None
        The roots
    """

    discriminant = b**2 - 4.0*a*c
    if discriminant < 0.0:
        return None

    x_plus = (-b + sqrt(discriminant)) / (2.0*a)
    x_minus = (-b - sqrt(discriminant)) / (2.0*a)

    return x_plus, x_minus

We have changed the code, so now have to re-run all our tests, in case our change broke something else:

[25]:

print(real_quadratic_roots(1, 0, 1))
print(real_quadratic_roots(1, 0, 0))
print(real_quadratic_roots(1, 0, -1))

None
(0.0, 0.0)
(1.0, -1.0)

As a final test, we check what happens if the equation degenerates to a linear equation where 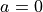$a=0$ , using 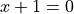$x + 1 = 0$ with solution $-1$ :

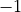[26]:

print(real_quadratic_roots(0, 1, 1))

---------------------------------------------------------------------------
ZeroDivisionError                         Traceback (most recent call last)
<ipython-input-26-e790de2bb87e> in <module>()
----> 1 print(real_quadratic_roots(0, 1, 1))

<ipython-input-24-a2282acd2dc3> in real_quadratic_roots(a, b, c)
     26         return None
     27
---> 28     x_plus = (-b + sqrt(discriminant)) / (2.0*a)
     29     x_minus = (-b - sqrt(discriminant)) / (2.0*a)
     30

ZeroDivisionError: float division by zero

In this case we get an exception, which we don’t want. We fix this problem:

[27]:

from math import sqrt

def real_quadratic_roots(a, b, c):
    """
    Find the real roots of the quadratic equation a x^2 + b x + c = 0, if they exist.

    Parameters
    ----------

    a : float
        Coefficient of x^2
    b : float
        Coefficient of x^1
    c : float
        Coefficient of x^0

    Returns
    -------

    roots : tuple or float or None
        The root(s) (two if a genuine quadratic, one if linear, None otherwise)

    Raises
    ------

    NotImplementedError
        If the equation has trivial a and b coefficients, so isn't solvable.
    """

    discriminant = b**2 - 4.0*a*c
    if discriminant < 0.0:
        return None

    if a == 0:
        if b == 0:
            raise NotImplementedError("Cannot solve quadratic with both a"
                                      " and b coefficients equal to 0.")
        else:
            return -c / b

    x_plus = (-b + sqrt(discriminant)) / (2.0*a)
    x_minus = (-b - sqrt(discriminant)) / (2.0*a)

    return x_plus, x_minus

And we now must re-run all our tests again, as the code has changed once more:

[28]:

print(real_quadratic_roots(1, 0, 1))
print(real_quadratic_roots(1, 0, 0))
print(real_quadratic_roots(1, 0, -1))
print(real_quadratic_roots(0, 1, 1))

None
(0.0, 0.0)
(1.0, -1.0)
-1.0

Formalizing tests¶

This small set of tests covers most of the cases we are concerned with. However, by this point it’s getting hard to remember

what each line is actually testing, and
what the correct value is meant to be.

To formalize this, we write each test as a small function that contains this information for us. Let’s start with the 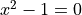$x^2 - 1 = 0$ case where the roots are $\pm 1$ :

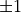[29]:

from numpy.testing import assert_equal, assert_allclose

def test_real_distinct():
    """
    Test that the roots of x^2 - 1 = 0 are \pm 1.
    """

    roots = (1.0, -1.0)
    assert_equal(real_quadratic_roots(1, 0, -1), roots,
                 err_msg="Testing x^2-1=0; roots should be 1 and -1.")

[30]:

test_real_distinct()

What this function does is checks that the results of the function call match the expected value, here stored in roots. If it didn’t match the expected value, it would raise an exception:

[31]:

def test_should_fail():
    """
    Comparing the roots of x^2 - 1 = 0 to (1, 1), which should fail.
    """

    roots = (1.0, 1.0)
    assert_equal(real_quadratic_roots(1, 0, -1), roots,
                 err_msg="Testing x^2-1=0; roots should be 1 and 1."
                 " So this test should fail")

test_should_fail()

---------------------------------------------------------------------------
AssertionError                            Traceback (most recent call last)
<ipython-input-31-ccb1cf91e65e> in <module>()
      9                  " So this test should fail")
     10
---> 11 test_should_fail()

<ipython-input-31-ccb1cf91e65e> in test_should_fail()
      6     roots = (1.0, 1.0)
      7     assert_equal(real_quadratic_roots(1, 0, -1), roots,
----> 8                  err_msg="Testing x^2-1=0; roots should be 1 and 1."
      9                  " So this test should fail")
     10

/Users/ih3/anaconda/lib/python3.4/site-packages/numpy/testing/utils.py in assert_equal(actual, desired, err_msg, verbose)
    288         assert_equal(len(actual), len(desired), err_msg, verbose)
    289         for k in range(len(desired)):
--> 290             assert_equal(actual[k], desired[k], 'item=%r\n%s' % (k, err_msg), verbose)
    291         return
    292     from numpy.core import ndarray, isscalar, signbit

/Users/ih3/anaconda/lib/python3.4/site-packages/numpy/testing/utils.py in assert_equal(actual, desired, err_msg, verbose)
    352     # Explicitly use __eq__ for comparison, ticket #2552
    353     if not (desired == actual):
--> 354         raise AssertionError(msg)
    355
    356 def print_assert_equal(test_string, actual, desired):

AssertionError:
Items are not equal:
item=1
Testing x^2-1=0; roots should be 1 and 1. So this test should fail
 ACTUAL: -1.0
 DESIRED: 1.0

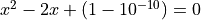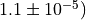Testing that one floating point number equals another can be dangerous. Consider $x^2 - 2 x + (1 - 10^{-10}) = 0$ with roots $1.1 \pm 10^{-5} )$ :

[32]:

from math import sqrt

def test_real_distinct_irrational():
    """
    Test that the roots of x^2 - 2 x + (1 - 10**(-10)) = 0 are 1 \pm 1e-5.
    """

    roots = (1 + 1e-5, 1 - 1e-5)
    assert_equal(real_quadratic_roots(1, -2.0, 1.0 - 1e-10), roots,
                 err_msg="Testing x^2-2x+(1-1e-10)=0; roots should be 1 +- 1e-5.")

test_real_distinct_irrational()

---------------------------------------------------------------------------
AssertionError                            Traceback (most recent call last)
<ipython-input-32-e01bced6ccc9> in <module>()
     10                  err_msg="Testing x^2-2x+(1-1e-10)=0; roots should be 1 +- 1e-5.")
     11
---> 12 test_real_distinct_irrational()

<ipython-input-32-e01bced6ccc9> in test_real_distinct_irrational()
      8     roots = (1 + 1e-5, 1 - 1e-5)
      9     assert_equal(real_quadratic_roots(1, -2.0, 1.0 - 1e-10), roots,
---> 10                  err_msg="Testing x^2-2x+(1-1e-10)=0; roots should be 1 +- 1e-5.")
     11
     12 test_real_distinct_irrational()

/Users/ih3/anaconda/lib/python3.4/site-packages/numpy/testing/utils.py in assert_equal(actual, desired, err_msg, verbose)
    288         assert_equal(len(actual), len(desired), err_msg, verbose)
    289         for k in range(len(desired)):
--> 290             assert_equal(actual[k], desired[k], 'item=%r\n%s' % (k, err_msg), verbose)
    291         return
    292     from numpy.core import ndarray, isscalar, signbit

/Users/ih3/anaconda/lib/python3.4/site-packages/numpy/testing/utils.py in assert_equal(actual, desired, err_msg, verbose)
    352     # Explicitly use __eq__ for comparison, ticket #2552
    353     if not (desired == actual):
--> 354         raise AssertionError(msg)
    355
    356 def print_assert_equal(test_string, actual, desired):

AssertionError:
Items are not equal:
item=0
Testing x^2-2x+(1-1e-10)=0; roots should be 1 +- 1e-5.
 ACTUAL: 1.0000100000004137
 DESIRED: 1.00001

We see that the solutions match to the first 14 or so digits, but this isn’t enough for them to be exactly the same. In this case, and in most cases using floating point numbers, we want the result to be “close enough”: to match the expected precision. There is an assertion for this as well:

[33]:

from math import sqrt

def test_real_distinct_irrational():
    """
    Test that the roots of x^2 - 2 x + (1 - 10**(-10)) = 0 are 1 \pm 1e-5.
    """

    roots = (1 + 1e-5, 1 - 1e-5)
    assert_allclose(real_quadratic_roots(1, -2.0, 1.0 - 1e-10), roots,
                 err_msg="Testing x^2-2x+(1-1e-10)=0; roots should be 1 +- 1e-5.")

test_real_distinct_irrational()

The assert_allclose statement takes options controlling the precision of our test.

We can now write out all our tests:

[34]:

from math import sqrt
from numpy.testing import assert_equal, assert_allclose

def test_no_roots():
    """
    Test that the roots of x^2 + 1 = 0 are not real.
    """

    roots = None
    assert_equal(real_quadratic_roots(1, 0, 1), roots,
                 err_msg="Testing x^2+1=0; no real roots.")

def test_zero_roots():
    """
    Test that the roots of x^2 = 0 are both zero.
    """

    roots = (0, 0)
    assert_equal(real_quadratic_roots(1, 0, 0), roots,
                 err_msg="Testing x^2=0; should both be zero.")

def test_real_distinct():
    """
    Test that the roots of x^2 - 1 = 0 are \pm 1.
    """

    roots = (1.0, -1.0)
    assert_equal(real_quadratic_roots(1, 0, -1), roots,
                 err_msg="Testing x^2-1=0; roots should be 1 and -1.")

def test_real_distinct_irrational():
    """
    Test that the roots of x^2 - 2 x + (1 - 10**(-10)) = 0 are 1 \pm 1e-5.
    """

    roots = (1 + 1e-5, 1 - 1e-5)
    assert_allclose(real_quadratic_roots(1, -2.0, 1.0 - 1e-10), roots,
                 err_msg="Testing x^2-2x+(1-1e-10)=0; roots should be 1 +- 1e-5.")

def test_real_linear_degeneracy():
    """
    Test that the root of x + 1 = 0 is -1.
    """

    root = -1.0
    assert_equal(real_quadratic_roots(0, 1, 1), root,
                 err_msg="Testing x+1=0; root should be -1.")

[35]:

test_no_roots()
test_zero_roots()
test_real_distinct()
test_real_distinct_irrational()
test_real_linear_degeneracy()

Nose¶

We now have a set of tests - a testsuite, as it is sometimes called - encoded in functions, with meaningful names, which give useful error messages if the test fails. Every time the code is changed, we want to re-run all the tests to ensure that our change has not broken the code. This can be tedious. A better way would be to run a single command that runs all tests. nosetests is that command.

The easiest way to use it is to put all tests in the same file as the function being tested. So, create a file quadratic.py containing

from math import sqrt
from numpy.testing import assert_equal, assert_allclose

def real_quadratic_roots(a, b, c):
    """
    Find the real roots of the quadratic equation a x^2 + b x + c = 0, if they exist.

    Parameters
    ----------

    a : float
        Coefficient of x^2
    b : float
        Coefficient of x^1
    c : float
        Coefficient of x^0

    Returns
    -------

    roots : tuple or float or None
        The root(s) (two if a genuine quadratic, one if linear, None otherwise)

    Raises
    ------

    NotImplementedError
        If the equation has trivial a and b coefficients, so isn't solvable.
    """

    discriminant = b**2 - 4.0*a*c
    if discriminant < 0.0:
        return None

    if a == 0:
        if b == 0:
            raise NotImplementedError("Cannot solve quadratic with both a"
                                      " and b coefficients equal to 0.")
        else:
            return -c / b

    x_plus = (-b + sqrt(discriminant)) / (2.0*a)
    x_minus = (-b - sqrt(discriminant)) / (2.0*a)

    return x_plus, x_minus

def test_no_roots():
    """
    Test that the roots of x^2 + 1 = 0 are not real.
    """

    roots = None
    assert_equal(real_quadratic_roots(1, 0, 1), roots,
                 err_msg="Testing x^2+1=0; no real roots.")

def test_zero_roots():
    """
    Test that the roots of x^2 = 0 are both zero.
    """

    roots = (0, 0)
    assert_equal(real_quadratic_roots(1, 0, 0), roots,
                 err_msg="Testing x^2=0; should both be zero.")

def test_real_distinct():
    """
    Test that the roots of x^2 - 1 = 0 are \pm 1.
    """

    roots = (1.0, -1.0)
    assert_equal(real_quadratic_roots(1, 0, -1), roots,
                 err_msg="Testing x^2-1=0; roots should be 1 and -1.")

def test_real_distinct_irrational():
    """
    Test that the roots of x^2 - 2 x + (1 - 10**(-10)) = 0 are 1 \pm 1e-5.
    """

    roots = (1 + 1e-5, 1 - 1e-5)
    assert_allclose(real_quadratic_roots(1, -2.0, 1.0 - 1e-10), roots,
                 err_msg="Testing x^2-2x+(1-1e-10)=0; roots should be 1 +- 1e-5.")

def test_real_linear_degeneracy():
    """
    Test that the root of x + 1 = 0 is -1.
    """

    root = -1.0
    assert_equal(real_quadratic_roots(0, 1, 1), root,
                 err_msg="Testing x+1=0; root should be -1.")

Then, in a terminal or command window, switch to the directory containing this file. Then run

nosetests quadratic.py

You should see output similar to

nosetests quadratic.py
.....
----------------------------------------------------------------------
Ran 5 tests in 0.006s

OK

Each dot corresponds to a test. If a test fails, nose will report the error and move on to the next test. nose automatically runs every function that starts with test, or every file in a module starting with test, or more. The documentation gives more details about using nose in more complex cases.

To summarize: when trying to get code working, tests are essential. Tests should be simple and cover as many of the easy cases and as much of the code as possible. By writing tests as functions that raise exceptions, and using a testing framework such as nose, all tests can be run rapidly, saving time.

Test Driven Development¶

There are many ways of writing code to solve problems. Most involve planning in advance how the code should be written. An alternative is to say in advance what tests the code should pass. This Test Driven Development (TDD) has advantages (the code always has a detailed set of tests, features in the code are always relevant to some test, it’s easy to start writing code) and some disadvantages (it can be overkill for small projects, it can lead down blind alleys). A detailed discussion is given by Beck’s book, and a more recent discussion in this series of conversations.

Even if TDD does not work for you, testing itself is extremely important.