Classes and Object Oriented Programming

We have looked at functions which take input and return output (or do things to the input). However, sometimes it is useful to think about objects first rather than the actions applied to them.

Think about a polynomial, such as the cubic

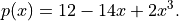
This is one of the standard forms that we would expect to see for a polynomial. We could imagine representing this in Python using a container containing the coefficients, such as:

p_normal = (12, -14, 0, 2)

The order of the polynomial is given by the number of coefficients (minus one), which is given by len(p_normal)-1.

However, there are many other ways it could be written, which are useful in different contexts. For example, we are often interested in the roots of the polynomial, so would want to express it in the form

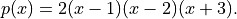
This allows us to read off the roots directly. We could imagine representing this in Python using a container containing the roots, such as:

p_roots = (1, 2, -3)

combined with a single variable containing the leading term,

p_leading_term = 2

We see that the order of the polynomial is given by the number of roots (and hence by len(p_roots)). This form represents the same polynomial but requires two pieces of information (the roots and the leading coefficient).

The different forms are useful for different things. For example, if we want to add two polynomials the standard form makes it straightforward, but the factored form does not. Conversely, multiplying polynomials in the factored form is easy, whilst in the standard form it is not.

But the key point is that the object - the polynomial - is the same: the representation may appear different, but it’s the object itself that we really care about. So we want to represent the object in code, and work with that object.

Classes

Python, and other languages that include object oriented concepts (which is most modern languages) allow you to define and manipulate your own objects. Here we will define a polynomial object step by step.

class Polynomial(object):
    explanation = "I am a polynomial"

    def explain(self):
        print(self.explanation)

We have defined a class, which is a single object that will represent a polynomial. We use the keyword class in the same way that we use the keyword def when defining a function. The definition line ends with a colon, and all the code defining the object is indented by four spaces.

The name of the object - the general class, or type, of the thing that we’re defining - is Polynomial. The convention is that class names start with capital letters, but this convention is frequently ignored.

The type of object that we are building on appears in brackets after the name of the object. The most basic thing, which is used most often, is the object type as here.

Class variables are defined in the usual way, but are only visible inside the class. Variables that are set outside of functions, such as explanation above, will be common to all class variables.

Functions are defined inside classes in the usual way (using the def keyword, indented by four additional spaces). They work in a special way: they are not called directly, but only when you have a member of the class. This is what the self keyword does: it takes the specific instance of the class and uses its data. Class functions are often called methods.

Let’s see how this works on a specific example:

p = Polynomial()
print(p.explanation)
p.explain()
p.explanation = "I change the string"
p.explain()

I am a polynomial
I am a polynomial
I change the string

The first line, p = Polynomial(), creates an instance of the class. That is, it creates a specific Polynomial. It is assigned to the variable named p. We can access class variables using the “dot” notation, so the string can be printed via p.explanation. The method that prints the class variable also uses the “dot” notation, hence p.explain(). The self variable in the definition of the function is the instance itself, p. This is passed through automatically thanks to the dot notation.

Note that we can change class variables in specific instances in the usual way (p.explanation = ... above). This only changes the variable for that instance. To check that, let us define two polynomials:

p = Polynomial()
p.explanation = "Changed the string again"
q = Polynomial()
p.explanation = "Changed the string a third time"
p.explain()
q.explain()

Changed the string a third time
I am a polynomial

We can of course make the methods take additional variables. We modify the class (note that we have to completely re-define it each time):

class Polynomial(object):
    explanation = "I am a polynomial"

    def explain_to(self, caller):
        print("Hello, {}. {}.".format(caller,self.explanation))

We then use this, remembering that the self variable is passed through automatically:

r = Polynomial()
r.explain_to("Alice")

Hello, Alice. I am a polynomial.

At the moment the class is not doing anything interesting. To do something interesting we need to store (and manipulate) relevant variables. The first thing to do is to add those variables when the instance is actually created. We do this by adding a special function (method) which changes how the variables of type Polynomial are created:

class Polynomial(object):
    """Representing a polynomial."""
    explanation = "I am a polynomial"

    def __init__(self, roots, leading_term):
        self.roots = roots
        self.leading_term = leading_term
        self.order = len(roots)

    def explain_to(self, caller):
        print("Hello, {}. {}.".format(caller,self.explanation))
        print("My roots are {}.".format(self.roots))

This __init__ function is called when a variable is created. There are a number of special class functions, each of which has two underscores before and after the name. This is another Python convention that is effectively a rule: functions surrounded by two underscores have special effects, and will be called by other Python functions internally. So now we can create a variable that represents a specific polynomial by storing its roots and the leading term:

p = Polynomial(p_roots, p_leading_term)
p.explain_to("Alice")
q = Polynomial((1,1,0,-2), -1)
q.explain_to("Bob")

Hello, Alice. I am a polynomial.
My roots are (1, 2, -3).
Hello, Bob. I am a polynomial.
My roots are (1, 1, 0, -2).

It is always useful to have a function that shows what the class represents, and in particular what this particular instance looks like. We can define another method that explicitly displays the Polynomial:

class Polynomial(object):
    """Representing a polynomial."""
    explanation = "I am a polynomial"

    def __init__(self, roots, leading_term):
        self.roots = roots
        self.leading_term = leading_term
        self.order = len(roots)

    def display(self):
        string = str(self.leading_term)
        for root in self.roots:
            if root == 0:
                string = string + "x"
            elif root > 0:
                string = string + "(x - {})".format(root)
            else:
                string = string + "(x + {})".format(-root)
        return string

    def explain_to(self, caller):
        print("Hello, {}. {}.".format(caller,self.explanation))
        print("My roots are {}.".format(self.roots))

p = Polynomial(p_roots, p_leading_term)
print(p.display())
q = Polynomial((1,1,0,-2), -1)
print(q.display())

2(x - 1)(x - 2)(x + 3)
-1(x - 1)(x - 1)x(x + 2)

Where classes really come into their own is when we manipulate them as objects in their own right. For example, we can multiply together two polynomials to get another polynomial. We can create a method to do that:

class Polynomial(object):
    """Representing a polynomial."""
    explanation = "I am a polynomial"

    def __init__(self, roots, leading_term):
        self.roots = roots
        self.leading_term = leading_term
        self.order = len(roots)

    def display(self):
        string = str(self.leading_term)
        for root in self.roots:
            if root == 0:
                string = string + "x"
            elif root > 0:
                string = string + "(x - {})".format(root)
            else:
                string = string + "(x + {})".format(-root)
        return string

    def multiply(self, other):
        roots = self.roots + other.roots
        leading_term = self.leading_term * other.leading_term
        return Polynomial(roots, leading_term)

    def explain_to(self, caller):
        print("Hello, {}. {}.".format(caller,self.explanation))
        print("My roots are {}.".format(self.roots))

p = Polynomial(p_roots, p_leading_term)
q = Polynomial((1,1,0,-2), -1)
r = p.multiply(q)
print(r.display())

-2(x - 1)(x - 2)(x + 3)(x - 1)(x - 1)x(x + 2)

We now have a simple class that can represent polynomials and multiply them together, whilst printing out a simple string form representing itself. This can obviously be extended to be much more useful.

Exercise: Equivalence classes

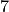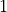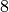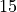An equivalence class is a relation that groups objects in a set into related subsets. For example, if we think of the integers modulo , then is in the same equivalence class as (and , and 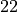, and so on), and 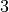is in the same equivalence class as 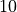. We use the tilde 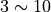to denote two objects within the same equivalence class.

Here, we are going to define the positive integers programmatically from equivalent sequences.

Exercise 1

Define a Python class Eqint. This should be

1. Initialized by a sequence;
2. Store the sequence;
3. Have a display method that returns a string showing the integer length of the sequence;
4. Have an equals method that checks if two Eqints are equal, which is True if, and only if, their sequences have the same length.

Exercise 2

Define a zero object from the empty list, and three one objects, from a single object list, tuple, and string. For example

one_list = Eqint([1])
one_tuple = Eqint((1,))
one_string = Eqint('1')

Check that none of the one objects equal the zero object, but all equal the other one objects. Display each object to check that the representation gives the integer length.

Exercise 3

Redefine the class by including an add method that combines the two sequences. That is, if a and b are Eqints then a.add(b) should return an Eqint defined from combining a and bs sequences.

Note

Adding two different types of sequences (eg, a list to a tuple) does not work, so it is better to either iterate over the sequences, or to convert to a uniform type before adding.

Exercise 4

Check your addition function by adding together all your previous Eqint objects (which will need re-defining, as the class has been redefined). Display the resulting object to check you get 3, and also print its internal sequence.

Exercise 5

We will sketch a construction of the positive integers from nothing.

1. Define an empty list positive_integers.
2. Define an Eqint called zero from the empty list. Append it to positive_integers.
3. Define an Eqint called next_integer from the Eqint defined by a copy of positive_integers (ie, use Eqint(list(positive_integers)). Append it to positive_integers.
4. Repeat step 3 as often as needed.

Use this procedure to define the Eqint equivalent to 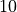. Print it, and its internal sequence, to check.